How HOMER Calculates Wind Turbine Power Output

HOMER calculates the power output of the wind turbine in each time step using a three-step process:

1. Calculate the wind speed at the hub height of the wind turbine.
2. Calculate the power output at that wind speed under standard air density.
3. Adjust that power output for the actual air density.

---

Calculating Hub Height Wind Speed

In each time step, HOMER calculates the wind speed at the hub height of the wind turbine using the inputs you specify in the Wind Resource page and the Wind Shear entry.

If you choose to apply the logarithmic law, HOMER calculates the hub height wind speed using:

$$U_{\text{hub}} = U_{\text{anem}} \cdot \frac{\ln\left(\frac{z_{\text{hub}}}{z_0}\right)} {\ln\left(\frac{z_{\text{anem}}}{z_0}\right)}$$

where:

• U_hub = wind speed at the hub height of the wind turbine [m/s]
• U_anem = wind speed at anemometer height [m/s]
• z_hub = hub height of the wind turbine [m]
• z_anem = anemometer height [m]
• z₀ = surface roughness length [m]
• ln(..) = natural logarithm

---

If you choose to apply the power law, HOMER calculates the hub height wind speed using:

$$U_{\text{hub}} = U_{\text{anem}} \left( \frac{z_{\text{hub}}}{z_{\text{anem}}} \right)^{\alpha}$$

where:

• U_hub = wind speed at the hub height of the wind turbine [m/s]
• U_anem = wind speed at anemometer height [m/s]
• z_hub = hub height of the wind turbine [m]
• z_anem = anemometer height [m]
• α = power law exponent

---

Calculating Turbine Power Output at Standard Air Density

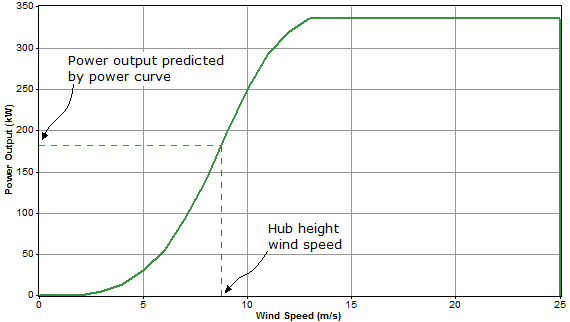
Once the hub height wind speed is determined, HOMER refers to the wind turbine’s power curve to calculate the expected power output at that wind speed under standard conditions of temperature and pressure.

If the wind speed at the turbine hub height is not within the range defined in the power curve, the turbine produces no power — assuming wind turbines produce no power at speeds below the cut-in speed or above the cut-out speed.

---

Applying Density Correction

Power curves typically specify wind turbine performance under standard temperature and pressure (STP).
To adjust to actual conditions, HOMER multiplies the power predicted by the power curve by the air density ratio:

$$P_{\text{WTG}} = \left( \frac{\rho}{\rho_0} \right) P_{\text{WTG,STP}}$$

where:

• P_WTG = wind turbine power output [kW]
• P_WTG,STP = wind turbine power output at standard temperature and pressure [kW]
• ρ = actual air density [kg/m³]
• ρ₀ = air density at standard temperature and pressure = 1.225 [kg/m³]

---

This process allows HOMER to model realistic turbine performance based on site-specific atmospheric conditions.